Lp自体を考えていきましょう.
まずは,曲げモーメントが加わった場合の物質のたわみを考えていきます.

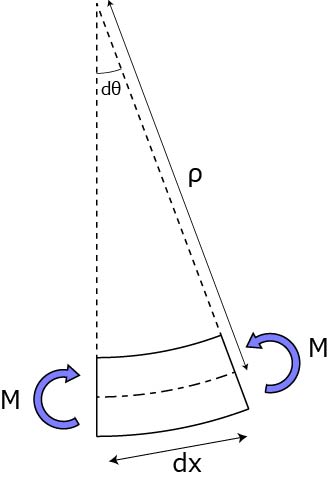
物質の断片を考えると,曲げモーメントが加わった場合,物質は円弧を描くと近似できます.
円弧の半径をρ,断片のなす角度をdθ,とおきます.
断片の長さ,dx,との関係は,
![]()
となります.
その微小領域を考えると,
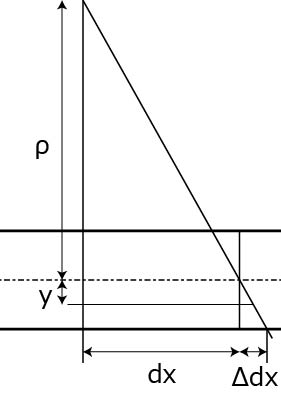
のようになります.
ここで,
ρ:半径
dx:断片の長さ
Δdx:断片の伸び
y:断片のある領域の中心からの距離
です.
ひずみの関係式,から,
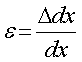
相似の関係から,
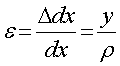
となります.
ヤング率の項で示したように,
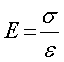
となりますので,
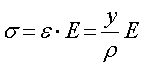
となります.
微小曲げモーメントはここで説明したように,
![]()
となりますので,全曲げモーメントは,
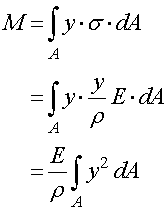
となります.ここで,積分項は,ここ,で説明したように,断面二次モーメントとなりますので,
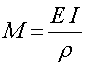
となります.
次ページに行きます.